python机器学习数据建模与分析数据预测与预测建模

更新时间：2026-02-15 12:28:31

爱情和生活模拟rpg手机版

类型：体育竞技
大小：87.5mb
语言：简体中文
评分：

查看详情

python机器学习数据建模与分析数据预测与预测建模

大数据时代的到来推动了机器学习预测建模技术迅速发展。利用机器学习算法对大量数据进行分析与建模，可预测未来的趋势和结果。该方法已在金融、医疗、交通及电子商务等领域得到广泛应用。随着人们对数据需求的增加以及计算机处理能力和算法的发展，机器学习预测建模已成为数据分析决策制定的重要工具。

项目背景

人工智能预测模型是指通过机器学习算法分析现有的数据来预测未来的趋势和结果。这种方法已经广泛应用于金融、医疗、交通和电子商务等领域。随着对信息需求的增加以及计算机处理能力和算法进步，机器学习成为数据分析和决策制定的关键工具。在大数据时代，机器学习预测建模已成为不可或缺的一部分。

在机器学习中，预测建模是一个重要的环节，特别是在选择模型这一过程中。模型的选择对于机器学习预测建模的效果至关重要。正确的模型选择直接影响到预测的准确性和效果。在模型选择的过程中，需要考虑的因素包括但不限于模型的性能、泛化能力、计算成本以及数据量等。在进行模型选择时，首先需要评估模型的性能指标，例如准确率、精度、召回率和F数，这些指标可以帮助我们了解模型对不同任务的适应性及其预测结果的质量。除了上述性能指标外，还需要注意的是模型的选择不应仅限于关注其预测能力。例如，一个高准确率但低召回率的模型可能在实际应用中表现不佳，因为这可能导致大量的假阳性问题。因此，在选择模型时，还需综合考虑预测的精准性和召回能力，确保模型能够在不同的场景下都表现出色。总之，选择合适的机器学习模型是构建有效预测建模的关键步骤。通过对模型的性能、泛化能力和数据需求等方面的全面考量，我们可以为不同任务找到最匹配的解决方案。

数据预测，简而言之就是基于已有数据集，归纳出输入变量和输出变量之间的数量关系。基于这种数量关系: 一方面，可发现对输出变量产生重要影响的输入变量；另一方面，在数量关系具有普适性和未来不变的假设下，可用于对新数据输出变量取值的预测。对数值型输出变量的预测称为回归。对分类型输出变量的预测称为分类

数据预测涉及的问题：第一，预测建模第二，模型评价第三，模型选择

一、预测建模

1.1 预测建模涉及的方面

第一，预测模型的形式第二，预测模型的几何意义第三，模型参数的估计

什么是预测模型？

立即学习“Python免费学习笔记（深入）”！预测模型通常用数学语言表达，准确捕捉并描述输入变量与输出变量之间数量关系。这类模型又细分为两种类型：回归预测模型用于解决分类问题，而分类预测模型则适用于处理回归问题。

y=β0+β1X1+β2X2+...+βpXp+εy=β0+β1X1+β2X2+...+βpXp+ε 分类预测模型：

log(P1P)=β0+β1X1+β2X2+...+βpXp+εlog(1PP)=β0+β1X1+β2X2+...+βpXp+ε 用于预测的回归方程：

y^=β0^+β1^X1+β2^X2+...+βp^Xpy^=β0^+β1^X1+β2^X2+...+βp^Xp

LogitP^=log(P^1P^)=β0^+β1^X1+β2^X2+...+βp^XpLogitP^=log(1P^P^)=β0^+β1^X1+β2^X2+...+βp^Xp

预测模型还有其他形式，如推理规则，它通过逻辑判断展示输入与输出变量间的规律。此外，还可以是推理规则集合及其图形化表现形式。

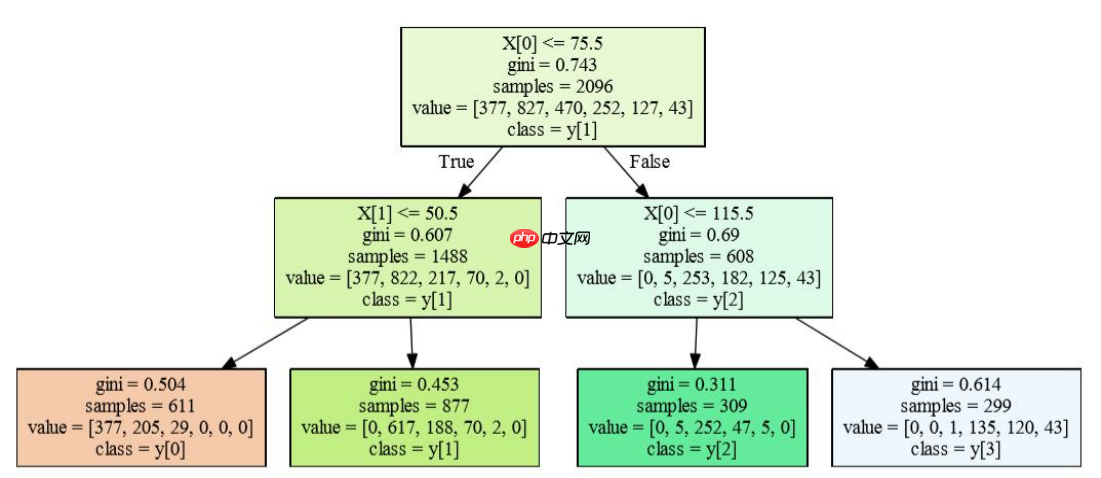
1.2 预测建模的几何理解

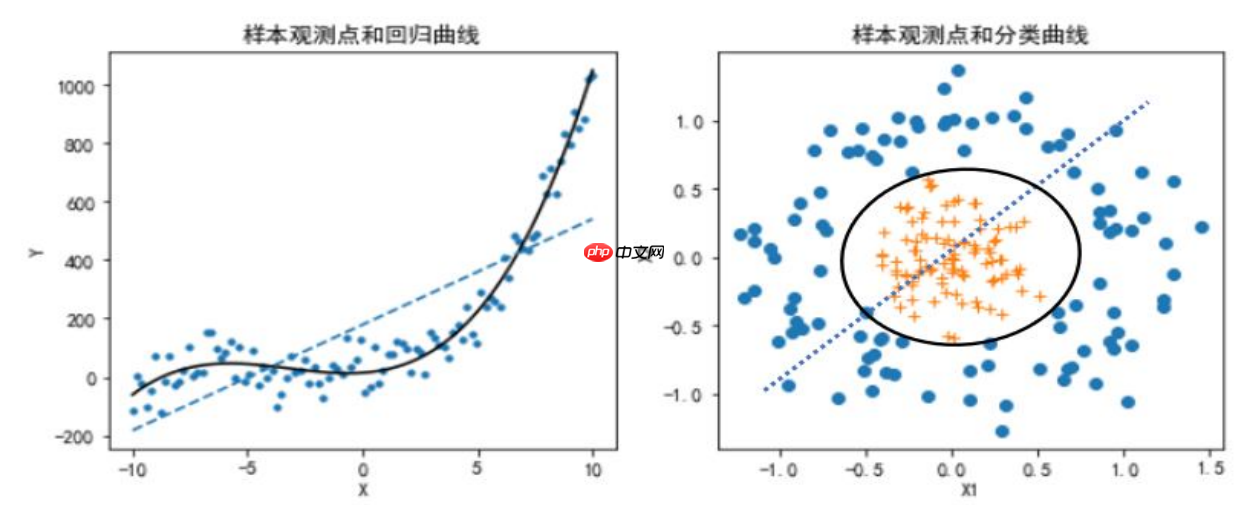
预测建模的出发点，是将数据集中的N个样本观测数据，视为pp维实数空间RpRp中的NN个点

回归预测模型：：回归直线回归平面

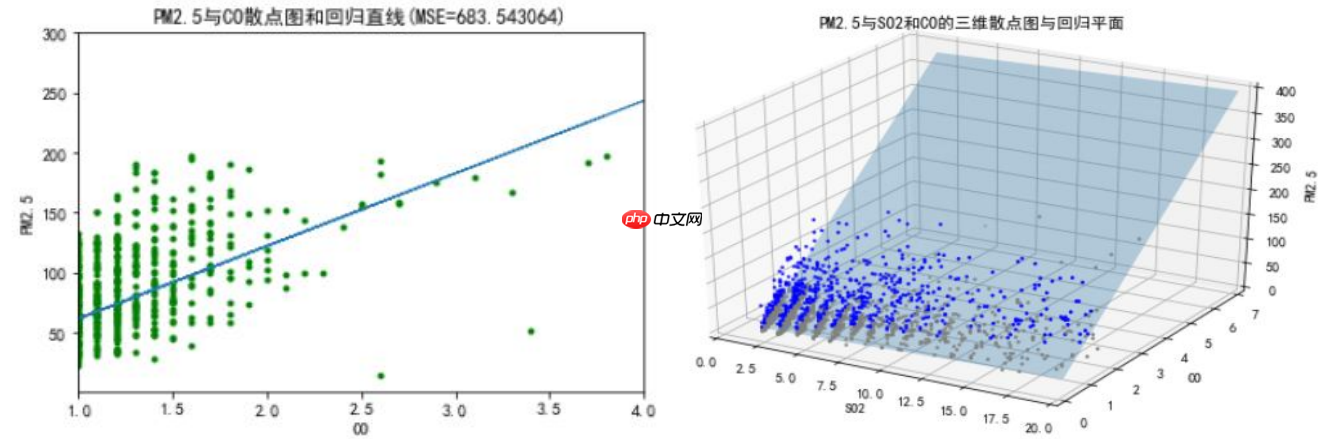
分类预测模型：分类直线分类平面

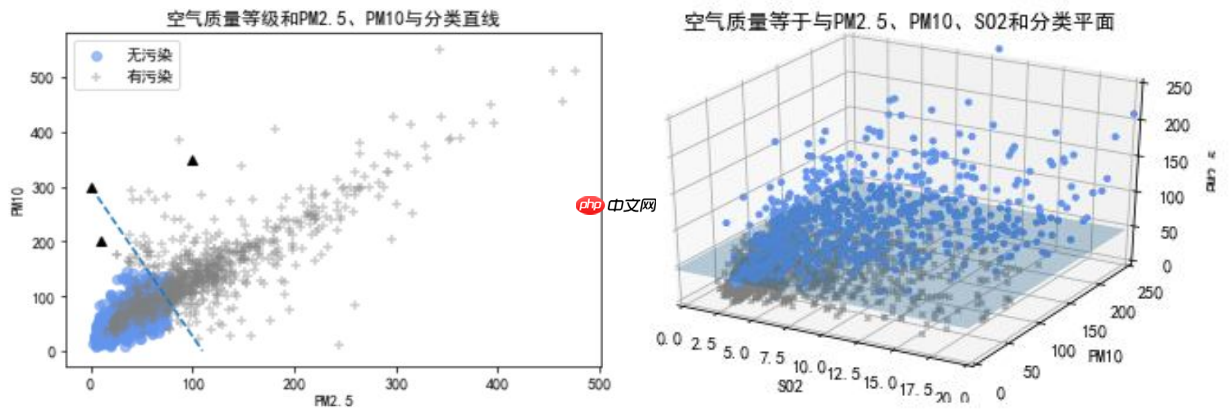
从直线到曲线，从平面到曲面

1.3 预测模型参数估计的基本策略

首先，目标是通过最小化损失函数来估计模型参数；其次，参数的确定常依赖于特定的优化策略。

1.4 有监督学习算法与损失函数

损失函数L是误差e的函数回归预测中的平方损失函数：

L(e)=L(yi,yi^)=(yiyi^)2L(e)=L(yi,yi^)=(yiyi^)2

∑i=1NL(yi,yi^)=∑i=1N(yiyi^)2i=1∑NL(yi,yi^)=i=1∑N(yiyi^)2 分类预测中的交互熵：

L(yi,pk^(Xi))=∑k=1KI(yi=k)log(Pk^(Xi))=logPyi^(Xi)L(yi,pk^(Xi))=k=1∑KI(yi=k)log(Pk^(Xi))=logPyi^(Xi) 二项偏差损失函数：

L(yi,f^(Xi))=yif^(Xi)+log(1+exp(f^(Xi)))L(yi,f^(Xi))=yif^(Xi)+log(1+exp(f^(Xi))) 指数损失函数：

L(yi,f^(Xi))=exp(yif^(Xi))L(yi,f^(Xi))=exp(yif^(Xi)) 多分类下的损失函数：

L(yi,fk^(Xi))=∑k=1KI(yi=k)log(exp(fk^(Xi))suml=1Kexp(fl^(Xi)))L(yi,fk^(Xi))=k=1∑KI(yi=k)log(suml=1Kexp(fl^(Xi))exp(fk^(Xi)))

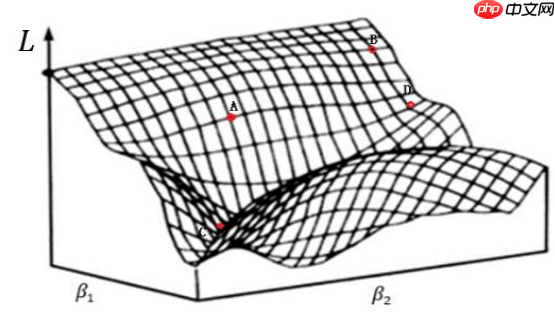
1.5 参数解空间和搜索策略

参数的最小二乘估计:

∑i=1NL(yi,yi^)=∑i=1NL(yi,f^(Xi))=∑i=1N(yi(β0^+β1^Xi1+β2^Xi2+...+βp^Xip))2i=1∑NL(yi,yi^)=i=1∑NL(yi,f^(Xi))=i=1∑N(yi(β0^+β1^Xi1+β2^Xi2+...+βp^Xip))2

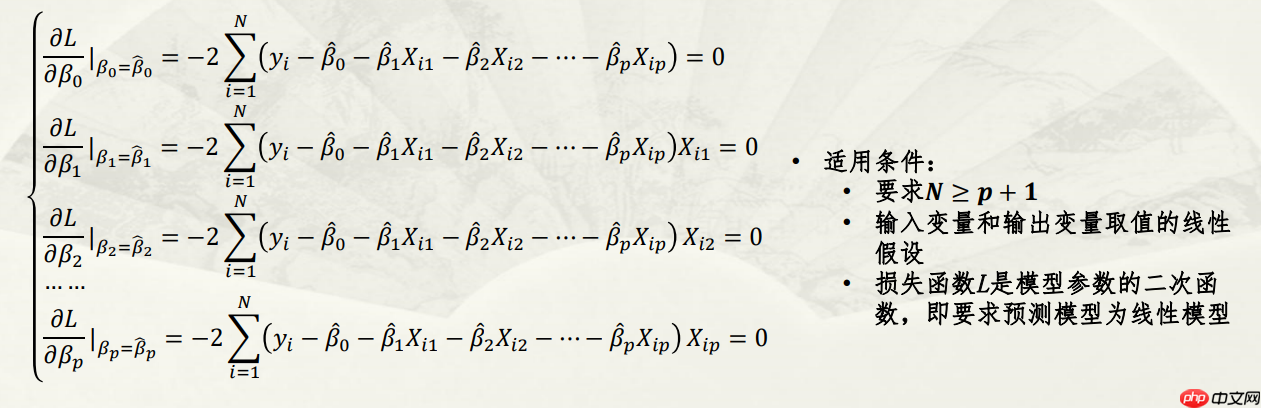
参数解空间和搜索策略：在预测模型参数解空间中，采用一定的搜索策略估计参数

梯度下降法

1.6 预测模型的评价

模型误差与预测误差概述模型误差（ModelError）：又称误差，是指基于训练数据对模型预测值和实际值的不一致程度度量。它包含两个部分：一是每个样本观测上的误差；二是整体数据集上误差的测量。预测误差或泛化误差（PredictiveError or GeneralizationError）：是指在使用模型进行新数据预测时，所得到的预测值与实际结果之间的差异。这个误差用来评估模型在未来新数据集中的预测能力。预测误差越低，意味着模型能够在广泛的场景中产生一般性和推广性，表明模型具有较高的泛化能力。结论两个概念共同关注的是模型在训练和测试过程中的表现如何影响其在实际应用中的效果。准确理解并控制这两个误差是提高机器学习模型可靠性和精度的关键步骤之一。

讨论的问题：第一，模型误差的评价指标第二，模型的图形化评价工具第三，泛化误差的估计方法

1.6.1 模型误差的评价指标

（1）回归预测模型中的误差评价指标：均方误差(MSE)

MSE=1N∑i=1N(yiyi^)2=E(L(yi,f^(Xi)))MSE=N1i=1∑N(yiyi^)2=E(L(yi,f^(Xi)))

（2）二分类预测模型中的误差评价指标

查准率(Precision)：Precision = TP / (TP + FP) 查全率(Recall)：Recall = TP / (TP + FN) 准确率(Accuracy)：Accuracy = TP + TN / (TP + TN + FP + FN) F数(Fscore)：Fscore = P×R / (P + R) 真正率(TPR)：TPR = TP / (TP + FN) 假正率(FPR)：FPR = TN / (TN + FP)

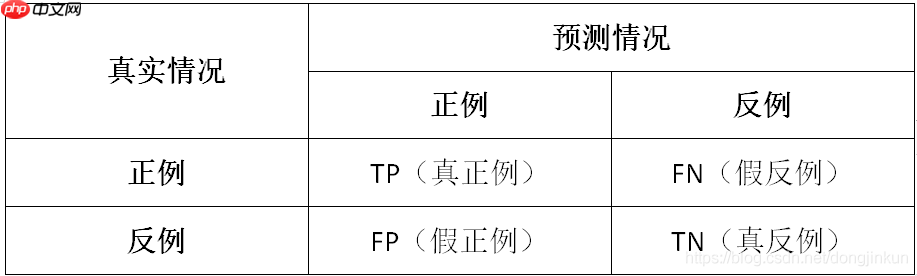
误判说明：TP：本应归类为正样本的正样本 TN：实际上属于负样本却被标记为负样本 FP：被错误判定为正样本的负样本 FN：预测为负样本但实际上属于正样本

通俗理解以西瓜数据集为例，我们将详细探讨TP、TN、FP和FN的含义：TP（True Positive）：被模型准确识别为好瓜的好瓜。这是我们所期望的结果。TN（True Negative）：被模型正确识别为坏瓜的坏瓜。这也是我们希望看到的情况。FP（False Positive）：被模型误判为好瓜的坏瓜。这是一种错误的预测结果，即实际上是坏瓜却被认为是好瓜。FN（False Negative）：被模型误判为坏瓜的好瓜。这是另一种错误，表示实际是好瓜却被模型判断为坏瓜。总的来说，TP和TN是正确的预测结果，FP和FN则代表了预测错误。这个理解有助于我们评估机器学习模型的性能，并找出可能需要改进的地方。

- 在多分类预测模型中，误差评估采用微平均和宏平均两种方式。前者基于所有类别，后者则分别计算每个类别的评价指标值。

1.6.2 模型的图形化评价工具

ROC曲线和AUG值 P-R曲线 In [3]

# 代码实现ROC曲线和P-R曲线import pandas as pdimport numpy as npfrom matplotlib import pyplot as plt %matplotlib inline#指定默认字体plt.rcParams['font.sans-serif']=['FZHuaLi-M14S'] plt.rcParams['axes.unicode_minus'] = Falsedata = pd.read_csv('类别和概率.csv') label=data['label'] prob=data['prob'] pos = np.sum(label == 1) neg = np.sum(label == 0) prob_sort = np.sort(prob)[::-1] index = np.argsort(prob)[::-1] label_sort = label[index] Pre = [] Rec = [] tpr=[] fpr=[]for i, item in enumerate(prob_sort): Rec.append(np.sum((label_sort[:(i+1)] == 1)) /pos) Pre.append(np.sum((label_sort[:(i+1)] == 1))/(i+1)) tpr.append(np.sum((label_sort[:(i+1)] == 1))/pos) fpr.append(np.sum((label_sort[:(i+1)] == 0)) /neg) fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4)) axes[0].plot(fpr,tpr,'k') axes[0].set_title('ROC曲线') axes[0].set_xlabel('FPR') axes[0].set_ylabel('TPR') axes[0].plot([0, 1], [0, 1], 'r--') axes[0].set_xlim([-0.01, 1.01]) axes[0].set_ylim([-0.01, 1.01]) axes[1].plot(Rec,Pre,'k') axes[1].set_title('P-R曲线') axes[1].set_xlabel('查全率R') axes[1].set_ylabel('查准率P') axes[1].plot([0,1],[1,pos/(pos+neg)], 'r--') axes[1].set_xlim([-0.01, 1.01]) axes[1].set_ylim([pos/(pos+neg)-0.01, 1.01])登录后复制

(0.455, 1.01)登录后复制

<Figure size 1000x400 with 2 Axes>登录后复制登录后复制登录后复制登录后复制登录后复制

ROC曲线

PR曲线

注意：AUC即为ROC曲线下的面积，而P-R曲线下的面积为AP值。mAP是多个类别AP的平均值，这个mean的意思是对每个类的AP再求平均，得到的就是mAP的值，mAP的大小一定在[区间内，越大越好。该指标是目标检测算法中最重要的一个指标。

1.6.3 训练误差和泛化误差

训练误差是指使用训练数据集构建模型后计算得出的误差值，也被称为经验误差或模型误差。此误差反映了对新样本的新预测与实际结果之间的偏差。

err=E(L(yi,f^(Xi)))=1Ntraining∑i=1Ntraining(yiyi^)2err=E(L(yi,f^(Xi)))=Ntraining1i=1∑Ntraining(yiyi^)2

训练误差的大小与模型复杂度和训练样本量有关

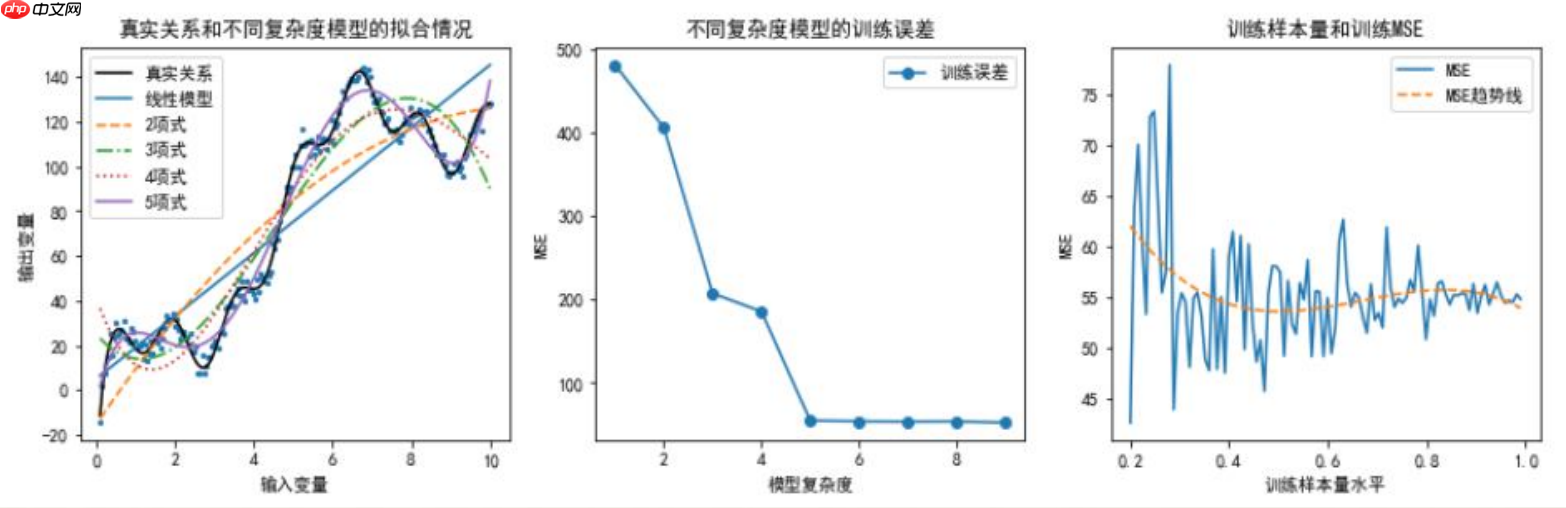
训练样本量和训练误差的理论关系

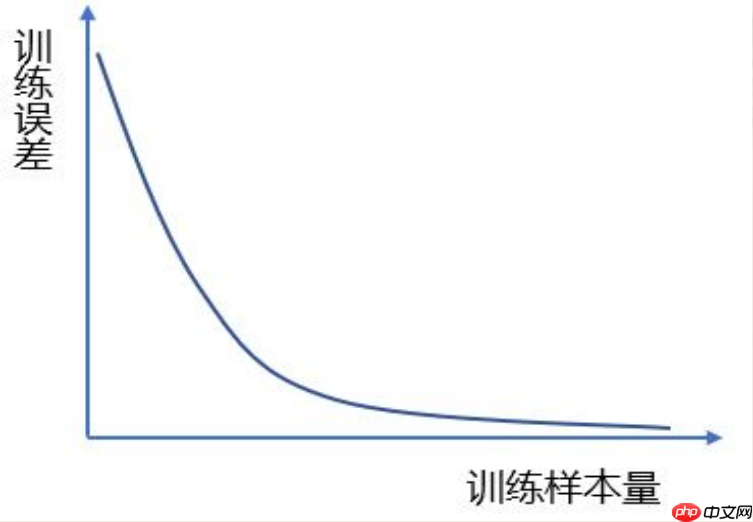
泛化误差难以直接测量：泛化误差是通过“袋外观测”来估算的，而非基于训练误差。损失函数最小化指导着参数估计：在最小化准则下，当前训练集中的最小值成为预测误差的基准。相比之下，在OOB评估中，该最低误差可能被低估。实践上，模型通常从数据集中随机抽取部分样本构建训练集（记为Τ），并将剩余样本用于测试。在这种情况下，计算出的测试误差实际上是基于OOB估算的泛化误差。

Err是针对N测试集中所有可能条件下的测试误差平滑计算结果，综合考虑了模型参数随训练数据变化的影响，揭示了模型对新实例的泛化能力。

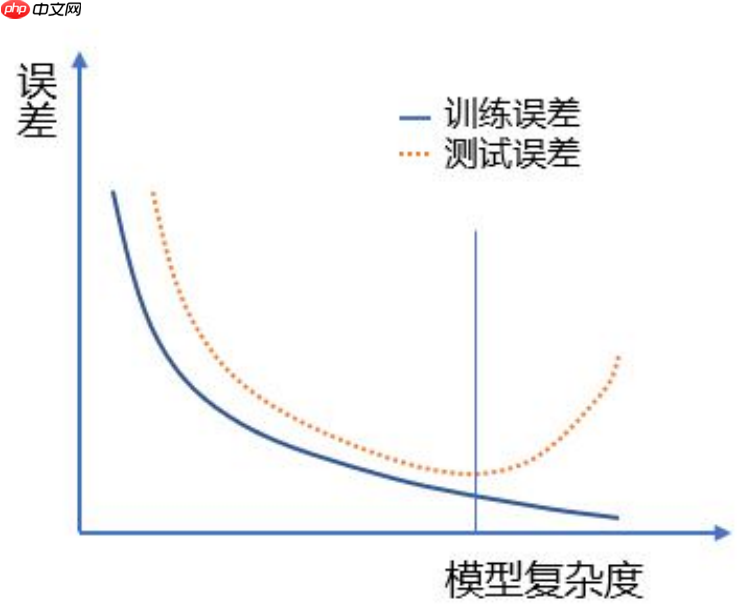
训练误差和测试误差的关系(单次随机划分和多次随机划分的情况)

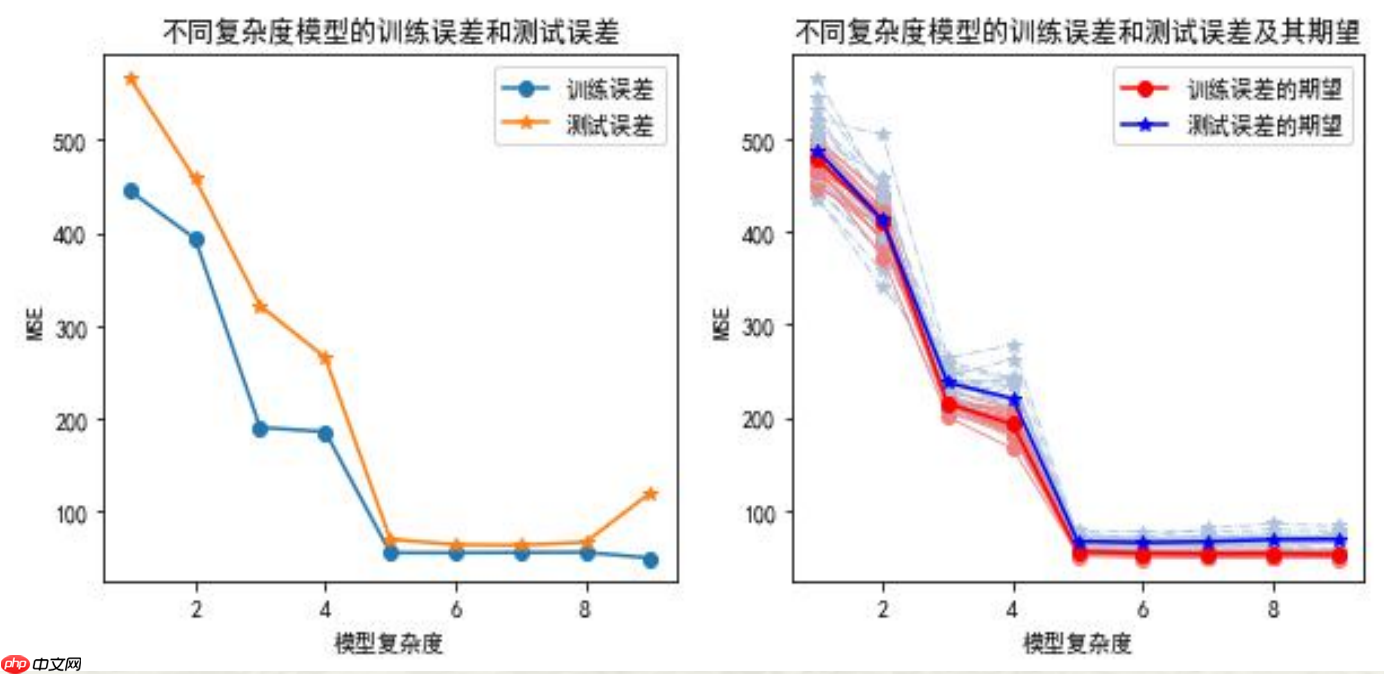
总结了训练误差和测试误差之间的关系：- 训练误差低估了泛化误差，所以应使用测试误差来估计泛化误差。- 随着训练错误的减小，预测模型并不一定总是最优的，因为最小时的测试误差不一定是最强的泛化能力模型。- 理想的预测模型应该是泛化能力和最小测试误差下的模型。

代码实现如下： In [6]

# 训练误差的大小与模型复杂度和训练样本量的关系图像# 导入所需模块import numpy as npimport pandas as pdimport matplotlib.pyplot as plt %matplotlib inline# 解决中文乱码问题plt.rcParams['font.sans-serif']=['FZHuaLi-M14S'] plt.rcParams['axes.unicode_minus'] = Falseimport warnings warnings.filterwarnings(action = 'ignore')from sklearn.metrics import confusion_matrix,f1_score,roc_curve, auc, precision_recall_curve,accuracy_scorefrom sklearn.model_selection import train_test_split,KFold,LeaveOneOut,LeavePOut # 数据集划分方法from sklearn.model_selection import cross_val_score,cross_validate # 计算交叉验证下的测试误差from sklearn import preprocessingimport sklearn.linear_model as LMfrom sklearn import neighbors np.random.seed(123) N=200x=np.linspace(0.1,10, num=N) y=[] z=[]for i in range(N): tmp=10*np.math.sin(4*x[i])+10*x[i]+20*np.math.log(x[i])+30*np.math.cos(x[i]) y.append(tmp) tmp=y[i]+np.random.normal(0,3) z.append(tmp) fig,axes=plt.subplots(nrows=1,ncols=3,figsize=(15,4)) axes[0].scatter(x,z,s=5) axes[0].plot(x,y,'k-',label="真实关系") modelLR=LM.LinearRegression() X=x.reshape(N,1) Y=np.array(z) modelLR.fit(X,Y) axes[0].plot(x,modelLR.predict(X),label="线性模型") linestyle=['--','-.',':','-']for i in np.arange(1,5): tmp=pow(x,(i+1)).reshape(N,1) X=np.hstack((X,tmp)) modelLR.fit(X,Y) axes[0].plot(x,modelLR.predict(X),linestyle=linestyle[i-1],label=str(i+1)+"项式") axes[0].legend() axes[0].set_title("真实关系和不同复杂度模型的拟合情况") axes[0].set_xlabel("输入变量") axes[0].set_ylabel("输出变量") X=x.reshape(N,1) Y=np.array(z) modelLR.fit(X,Y) MSEtrain=[np.sum((Y-modelLR.predict(X))**2)/(N-2)]for i in np.arange(1,9): tmp=pow(x,(i+1)).reshape(N,1) X=np.hstack((X,tmp)) modelLR.fit(X,Y) MSEtrain.append(np.sum((Y-modelLR.predict(X))**2)/(N-(i+2))) axes[1].plot(np.arange(1,10),MSEtrain,marker='o',label='训练误差') axes[1].legend() axes[1].set_title("不同复杂度模型的训练误差") axes[1].set_xlabel("模型复杂度") axes[1].set_ylabel("MSE") X=x.reshape(N,1) Y=np.array(z)for i in np.arange(1,5): #采用5项式模型 tmp=pow(x,(i+1)).reshape(N,1) X=np.hstack((X,tmp)) np.random.seed(0) size=np.linspace(0.2,0.99,100) MSEtrain=[]for i in range(len(size)): Ntraining=int(N*size[i]) id=np.random.choice(N,Ntraining,replace=False) X_train=X[id] y_train=Y[id] modelLR.fit(X_train,y_train) MSEtrain.append(np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-6)) tmpx=np.linspace(1,len(size), num=len(size)).reshape(len(size),1) #拟合MSEtmpX=np.hstack((tmpx,tmpx**2)) tmpX=np.hstack((tmpX,tmpx**3)) modelLR.fit(tmpX,MSEtrain) axes[2].plot(size,MSEtrain,linewidth=1.5,linestyle='-',label='MSE') axes[2].plot(size,modelLR.predict(tmpX),linewidth=1.5,linestyle='--',label='MSE趋势线') axes[2].set_title("训练样本量和训练MSE") axes[2].set_xlabel("训练样本量水平") axes[2].set_ylabel("MSE") axes[2].legend() plt.show()登录后复制

<Figure size 1500x400 with 3 Axes>登录后复制

说明：

在这一部分，我们借助数据仿真技术直观地展示了模型复杂度与训练误差之间的密切关系。随着模型复杂度的提升，训练误差呈现显著的递减趋势。

首先确定输入变量和输出变量的真实关系，并通过随机加入服从正态分布的随机数来模拟其他随机因素对输出变量的影响。在这种情况下，真实的函数模型可以通过泰勒展开来进行近似。随着阶数的增加（例如），参数估计的结果会逐渐趋近于实际观测值，但超出一定阈值之后，再继续增加阶数将不再显著提升预测精度，因此无需进一步增加阶数以提高准确性。

- 构建不同多项式的模型后，我们避免了由于简化问题所导致的MSE误差影响，并利用样本量与输入变量数量之差来计算分母，从而得到更准确的结果。

模型学习充分性与样本量的探索本研究考察了特定模型（例如五项式）在训练集上的学习充分性，并分析了样本量对其影响的程度。样本量由原数据集的到不等，以验证MSE计算中分母是否因样本量而受影响。通过三次曲线拟合，我们评估了不同样本量下MSE的变化趋势。这一方法确保了对MSE计算结果的影响最小化。

# 训练误差和测试误差的关系图像fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4)) modelLR=LM.LinearRegression() np.random.seed(123) Ntraining=int(N*0.7) Ntest=int(N*0.3)id=np.random.choice(N,Ntraining,replace=False) X_train=x[id].reshape(Ntraining,1) y_train=np.array(z)[id].reshape(Ntraining,1) modelLR.fit(X_train,y_train) MSEtrain=[np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-2)] xtest= np.delete(x, id).reshape(Ntest,1) X_test= np.delete(x, id).reshape(Ntest,1) y_test=np.delete(z,id).reshape(Ntest,1) MSEtest=[np.sum((y_test-modelLR.predict(X_test))**2)/(Ntest-2)]for i in np.arange(1,9): tmp=pow(x[id],(i+1)).reshape(Ntraining,1) X_train=np.hstack((X_train,tmp)) modelLR.fit(X_train,y_train) MSEtrain.append(np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-(i+2))) tmp=pow(xtest,(i+1)).reshape(Ntest,1) X_test=np.hstack((X_test,tmp)) MSEtest.append(np.sum((y_test-modelLR.predict(X_test))**2)/(Ntest-(i+2))) axes[0].plot(np.arange(1,10,1),MSEtrain,marker='o',label='训练误差') axes[0].plot(np.arange(1,10,1),MSEtest,marker='*',label='测试误差') axes[0].legend() axes[0].set_title("不同复杂度模型的训练误差和测试误差") axes[0].set_xlabel("模型复杂度") axes[0].set_ylabel("MSE") MSEtrain=[] MSEtest=[]for j in range(20): x=np.linspace(0.1,10, num=N) id=np.random.choice(N,Ntraining,replace=False) X_train=x[id].reshape(Ntraining,1) y_train=np.array(z)[id].reshape(Ntraining,1) modelLR.fit(X_train,y_train) mse_train=[np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-2)] xtest= np.delete(x, id).reshape(Ntest,1) X_test= np.delete(x, id).reshape(Ntest,1) y_test=np.delete(z,id).reshape(Ntest,1) mse_test=[np.sum((y_test-modelLR.predict(X_test))**2)/(Ntest-2)] for i in np.arange(1,9): tmp=pow(x[id],(i+1)).reshape(Ntraining,1) X_train=np.hstack((X_train,tmp)) modelLR.fit(X_train,y_train) mse_train.append(np.sum((y_train-modelLR.predict(X_train))**2)/(Ntraining-(i+2))) tmp=pow(xtest,(i+1)).reshape(Ntest,1) X_test=np.hstack((X_test,tmp)) mse_test.append(np.sum((y_test-modelLR.predict(X_test))**2)/(Ntest-(i+2))) plt.plot(np.arange(1,10),mse_train,marker='o',linewidth=0.8,c='lightcoral',linestyle='-') plt.plot(np.arange(1,10),mse_test,marker='*',linewidth=0.8,c='lightsteelblue',linestyle='-.') MSEtrain.append(mse_train) MSEtest.append(mse_test) MSETrain=pd.DataFrame(MSEtrain) MSETest=pd.DataFrame(MSEtest) axes[1].plot(np.arange(1,10),MSETrain.mean(),marker='o',linewidth=1.5,c='red',linestyle='-',label="训练误差的期望") axes[1].plot(np.arange(1,10),MSETest.mean(),marker='*',linewidth=1.5,c='blue',linestyle='-',label="测试误差的期望") axes[1].set_title("不同复杂度模型的训练误差和测试误差及其期望") axes[1].set_xlabel("模型复杂度") axes[1].set_ylabel("MSE") axes[1].legend() plt.show()登录后复制

<Figure size 1000x400 with 2 Axes>登录后复制登录后复制登录后复制登录后复制登录后复制

说明：

通过对数据进行仿真处理，清晰地展示了随着模型复杂度增加，在训练误差与测试误差之间的关系曲线变化过程。随着模型复杂度的提升，训练误差呈现直线式降低趋势；而测试误差则先减少后升高，形成典型的“U”型曲线。

在数据集上随机选择一部分作为训练数据进行模型训练，保留剩余部分用于验证模型性能，每次重复试验了。

样本观测进行随机抽取时必然导致训练集包含可能不同的样本观测，这使得模型参数估计值之间存在差异。因此，这些训练误差和测试误差的结果会有所不同。带圆点的浅红色和浅灰色代表抽样所得的训练误差与测试误差，它们的平均值则表现为红线和蓝线所示。

1.6.4 数据集的划分策略

训练误差可表述为：

CV(f^,α)=1N∑i=1NL(yi,f^k(i)(Xi,α))CV(f^,α)=N1i=1∑NL(yi,f^k(i)(Xi,α))

- $\alpha$表示人为指定的数据集划分策略。$\alpha$不同所导致的训练集不同将最终体现在预测模型上，因此将预测模型记为：$\hat{f}^{-k}(X,\alpha)$，表示第$\alpha$个预测模型（基于删去$k$部分数据之外的数据）登录后复制数据集的划分：旁置法（Hold out）留一法（Leave One Out， LOO） K折交叉验证法（K Cross-validation，CV）旁置法

在机器学习中，选择预测模型时遵循的基本原则之一是“奥克姆剃刀（Occam's Razor）”。这一原则强调了简单模型优于复杂的立场。通常情况下，简单模型的训练误差高于复杂模型，但若其泛化误差低于复杂模型，则应倾向于选择简单的模型。这个策略有助于在众多模型中找到最能准确描述数据特性的那一种。

预测模型中“佼佼者”需具备两大特质： - 高准确度训练结果 - 稳定且可靠预测能力。

选择复杂模型将导致怎样的后果？第一，模型过拟合（Over-Fitting）而导致的高泛化误差第二，模型过拟合而导致的低稳健性

模型过拟合是指在以最小化训练误差为目标的情况下，模型表现出的预测误差超过了对新数据的有效性。这通常表现为模型不仅能很好地学习到训练数据中的模式，而且还会过分记住这些具体的数据细节，而忽略了它们在实际应用中可能不再相关的部分。这种现象导致了在新的、未经训练的数据集上的表现较差即测试误差较大。过拟合是机器学习领域的一个重要概念，因为它影响着模型性能和泛化能力的关键问题。

2.1 不同复杂度模型下的拟合情况分析

In [10]

# 各种情况下的拟合np.random.seed(123) N=100x=np.linspace(-10,10, num=N) y=14+5.5*x+4.8*x**2+0.5*x**3z=[]for i in range(N): z.append(y[i]+np.random.normal(0,50)) fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4)) axes[0].scatter(x,z,s=10) axes[0].plot(x,y,'k-',label="真实关系") modelLR=LM.LinearRegression() X=x.reshape(N,1) Y=np.array(z) modelLR.fit(X,Y) axes[0].plot(x,modelLR.predict(X),linestyle='--',label="线性模型") linestyle=[':','-.'] degree=[2,3]for i in range(len(degree)): tmp=pow(x,degree[i]).reshape(N,1) X=np.hstack((X,tmp)) modelLR.fit(X,Y) axes[0].plot(x,modelLR.predict(X),linestyle=linestyle[i],label=str(degree[i])+"项式模型") KNNregr=neighbors.KNeighborsRegressor(n_neighbors=5) X=x.reshape(N,1) KNNregr.fit(X,Y) axes[0].plot(X,KNNregr.predict(X),linestyle='-',label="复杂模型") axes[0].legend() axes[0].set_title("真实关系和不同复杂度模型的拟合情况") axes[0].set_xlabel("输入变量") axes[0].set_ylabel("输出变量") X=x.reshape(N,1) Y=np.array(z) modelLR.fit(X,Y) np.random.seed(123) k=10scores = cross_validate(modelLR,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True) MSEtrain=[-1*scores['train_score'].mean()] MSEtest=[-1*scores['test_score'].mean()] degree=[2,3]for i in range(len(degree)): tmp=pow(x,degree[i]).reshape(N,1) X=np.hstack((X,tmp)) modelLR.fit(X,Y) scores = cross_validate(modelLR,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True) MSEtrain.append((-1*scores['train_score']).mean()) MSEtest.append((-1*scores['test_score']).mean()) KNNregr=neighbors.KNeighborsRegressor(n_neighbors=5) X=x.reshape(N,1) KNNregr.fit(X,Y) scores = cross_validate(KNNregr,X,Y, scoring='neg_mean_squared_error',cv=k, return_train_score=True) MSEtrain.append((-1*scores['train_score']).mean()) MSEtest.append((-1*scores['test_score']).mean()) axes[1].plot(np.arange(1,len(degree)+3),MSEtrain,marker='o',label='训练误差(10折交叉验证法)',linestyle='--') axes[1].plot(np.arange(1,len(degree)+3),MSEtest,marker='*',label='测试误差(10折交叉验证法)') axes[1].legend() axes[1].set_title("不同复杂度模型的训练误差和测试误差(Err)") axes[1].set_xlabel("模型复杂度") axes[1].set_ylabel("MSE") fig.show()登录后复制

<Figure size 1000x400 with 2 Axes>登录后复制登录后复制登录后复制登录后复制登录后复制

说明：

预测模型的偏差是指对新数据集中的样本X原始观测）进行预测时，模型给出的多个预测值y^（i= ...）的期望值E(y^)与其实际值y差异。这是一种衡量模型预测准确性的度量标准。理论上，预测偏差越小，表明模型对未知数据的泛化能力较强，泛化误差也较小。

预测模型的方差：指对新数据集中的样本观测$X_)，模型给出的多个预测值\(\hat{y}_{}$的方差，衡量了这些预测值在波动程度上的差异。理论上，方差越小意味着模型具有较好的鲁棒性，泛化误差的估计更加可靠和准确。

预测模型的偏差-方差分解：

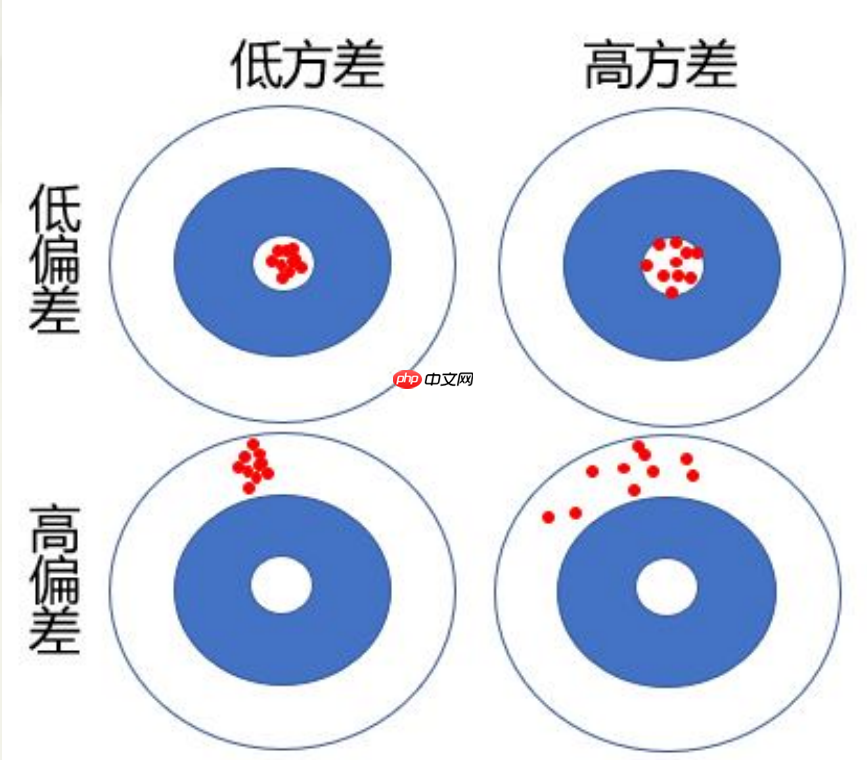
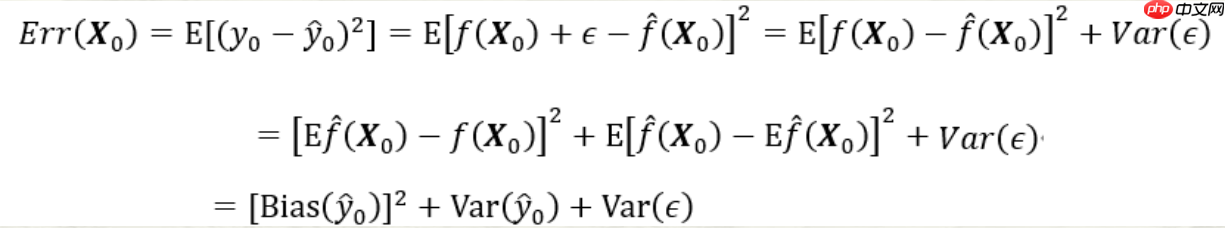
预测模型的偏差和方差关系首先，预测模型的误差由三个部分组成：随机误差项的方差σε第一项是上述偏差的平方（Bias^）；第二项是上述方差（Var）。第三项为随机误差项的方差。无论怎样调整模型，第三项都不会消失，除非σε第一项为预测值与真实值之间的平均差异的平方，度量了预测值与期望之间的偏差；第二项则衡量了预测值与其期望间的平均性差异。模型复杂度的影响模型复杂度增加时，预测误差的偏差会减少，但方差随之增加。如果偏差的减少能够抵消方差的增加，Err(X将趋于降低；反之，若偏差的减少无法与方差的增加相抵消，Err(X则会增加。在这一过程中，模型复杂度是关键因素之一。随着模型复杂度增加，预测误差通常表现为较大的偏差，而小方差。因此，保持适当的模型简单性和适度的复杂度对于控制预测误差至关重要。

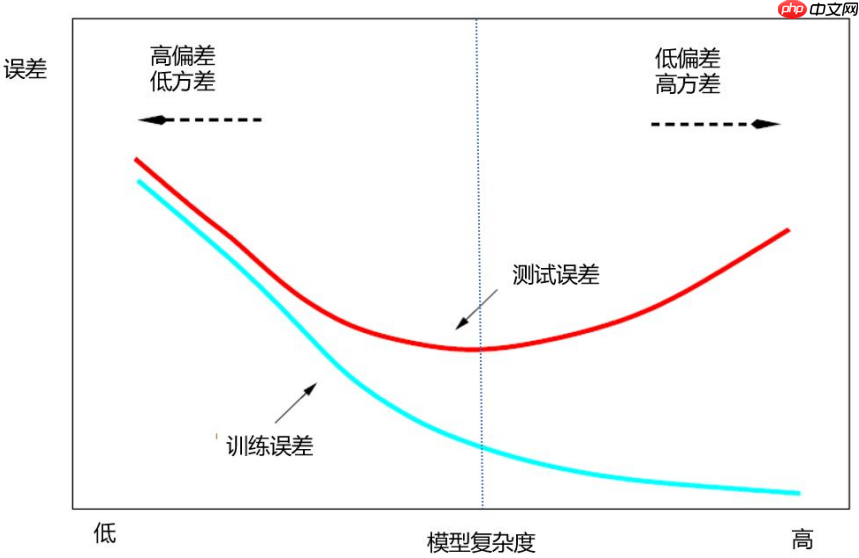
2.4 预测模型的偏差和方法的变化趋势

In [12]

在复杂的预测模型中，通过调整参数变化的偏差和方差趋势图展示。x[x.mean, x.mean x.mean构建了多元模型。对于不同复杂度的回归模型： LM线性回归模型： - Err = [np.var(model/np.mean(model, np.var(model/np.mean(model, np.var(model/np.mean(model] KNN神经网络分类器： - Err = [np.mean(model-y每个误差用方差计算，并对x行归一化处理，生成变化趋势图：- 偏差与方差：误差除以预测值的均值- 误差：误差平方后的根最终展示了不同复杂度模型的Err以及偏差和方差的变化趋势图。

<Figure size 600x400 with 1 Axes>登录后复制

三、综合应用：空气污染的分类预测

建立空气污染预测的Logistic回归模型 In [13]

加载北京市空气质量数据...处理缺失值...去除所有NA值...根据质量等级标记污染状态...计算并显示有无污染的频率分布...创建散点图，展示PMPM无污染和有污染的影响... 使用Logistic回归模型分析影响因素...通过截距项、回归系数以及优势比来评估模型表现... 预测结果为：总的错判率为：

- 1204 1 892 Name: 有无污染, dtype: int64 截距项:-4.858429 回归系数: [[0.05260358 0.01852681]] 优势比[[1.05401173 1.0186995 ]] 预测结果： [0 1 0 ... 0 0 0] 总的错判率：0.153149登录后复制

<Figure size 640x480 with 1 Axes>登录后复制

说明：在空气质量监测数据中，我们将质量等级为优和良的数据合并为无污染的一类（共），其余则为有污染一类（共）。本例中，我们仅考虑PMPM是否有污染的影响，并将其作为输入变量。输出变量是只有“无污染”或“有污染”的二分类问题。首先定义modelLR对象： ```python modelLR = LM.LogisticRegression ```然后使用fit方法拟合模型参数： ```python modelLR.fit(X, y) ``` 其中，X是输入变量（矩阵形式），y是输出变量。注意：这里的输入变量和输出变量需要按照预期的顺序进行处理。通过intercept_和coef_属性获取回归系数信息。从输出中可以看出，PM是否有污染的影响比PM显著： ```python print('Intercept： ', modelLR.intercept_) print('Coef for PM', modelLR.coef_[) print('Coef for PM', modelLR.coef_[) ```使用predict函数计算X的预测值：```python predictions = modelLR.predict(X) ``` 这将返回一个与输入变量X对应预测结果的列表，其中每个元素是“无污染”（或“有污染”（。为了优化模型并进行评估，请参阅文献[。

X=data.loc[:,['PM2.5','PM10','SO2','CO','NO2','O3']] Y=data.loc[:,'有无污染'] modelLR=LM.LogisticRegression() modelLR.fit(X,Y)print('训练误差:',1-modelLR.score(X,Y)) #print(accuracy_score(Y,modelLR.predict(X)))print('混淆矩阵:\n',confusion_matrix(Y,modelLR.predict(X)))print('F1-score:',f1_score(Y,modelLR.predict(X),pos_label=1)) fpr,tpr,thresholds = roc_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1) 计算fpr和tprroc_auc = auc(fpr,tpr) 计算auc的值print('AUC:',roc_auc)print('总正确率',accuracy_score(Y,modelLR.predict(X))) fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4)) axes[0].plot(fpr, tpr, color='r',linewidth=2, label='ROC curve (area = %0.5f)' % roc_auc) axes[0].plot([0, 1], [0, 1], color='navy', linewidth=2, linestyle='--') axes[0].set_xlim([-0.01, 1.01]) axes[0].set_ylim([-0.01, 1.01]) axes[0].set_xlabel('FPR') axes[0].set_ylabel('TPR') axes[0].set_title('ROC曲线') axes[0].legend(loc="lower right") pre, rec, thresholds = precision_recall_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1) axes[1].plot(rec, pre, color='r',linewidth=2, label='总正确率 = %0.3f)' % accuracy_score(Y,modelLR.predict(X))) axes[1].plot([0,1],[1,pre.min()],color='navy', linewidth=2, linestyle='--') axes[1].set_xlim([-0.01, 1.01]) axes[1].set_ylim([pre.min()-0.01, 1.01]) axes[1].set_xlabel('查全率R') axes[1].set_ylabel('查准率P') axes[1].set_title('P-R曲线') axes[1].legend(loc='lower left') plt.show()登录后复制

训练误差: 0.0782442748091603 混淆矩阵: [[1128 76] [ 88 804]] F1-score: 0.90744920993228 AUC: 0.982303010890455 总正确率 0.9217557251908397登录后复制

<Figure size 1000x400 with 2 Axes>登录后复制登录后复制登录后复制登录后复制登录后复制

空气质量预测与分析在当前空气质量监测数据中，采用Logistic回归模型对是否有污染进行分类预测是一个有效的方法。本研究使用了PMPMSOCO、NOO污染物浓度作为输入变量，同时有无污染作为输出变量（有污染，无污染）。我们通过此模型对实际数据进行了预测，并进一步分析其性能。为了评估模型的预测效果，使用了sklearn.metrics库中的confusion_matrix、fscore、roc_curve和auc等函数。这些函数可以用来计算混淆矩阵、F数、ROC曲线以及AUC值。具体来说：- modelLR.score(X, Y) 代表基于训练集的预测精度得分。 - accuracy_score(Y, modelLR.predict(X)) 可以直接计算预测正确率。此外，我们还使用了以下函数：- confusion_matrix(Y, modelLR.predict(X)) - fscore(Y, modelLR.predict(X), pos_label= - roc_curve - auc(fpr, tpr)这些方法有助于全面评估Logistic回归模型的性能。通过计算混淆矩阵、F数和AUC值，可以直观地了解模型预测的效果。ROC曲线与AUC值不仅表明了该模型的预测能力，还提供了详细的错误率对比信息（训练误差）。具体而言，ROC曲线展示了预测概率从大到小变化时的True Positive Rate (TPR) 和False Positive Rate (FPR)，而AUC值则是一个度量指标，用于衡量ROC曲线下的面积。通过精确地计算这些指标，我们可以发现本预测模型在分类预测中有显著的准确性，并且对训练数据的误差非常小。

以上就是python机器学习数据建模与分析数据预测与预测建模的详细内容，更多请关注其它相关文章！